【連載】基礎から応用までよくわかる組織透明化技術 「第5回 透明化技術と対物レンズ」
本記事は、和光純薬時報 Vol.88 No.2(2020年4月号)において、オリンパス株式会社 R&D 機能 光学システム開発 科学先進技術開発 理化学研究所 脳神経科学研究センター 理研 CBS-オリンパス連携センター 西脇 大介様、樋口 香織様に執筆いただいたものです。

はじめに
近年、固定組織の透明化技術の進展が目覚ましい。ここ10年の間に、様々な手法が開発され生命科学の発展に大きな影響を与えた。組織透明化は、これまで観察することが難しかった組織の 3 次元構造を、組織を破壊することなく、大規模・高精細に再構築することを可能とした(図 1)。こうした透明化の技術の発展に合わせて、透明化手法に対応した光学系、特に対物レンズも各メーカーから開発・発売されている。
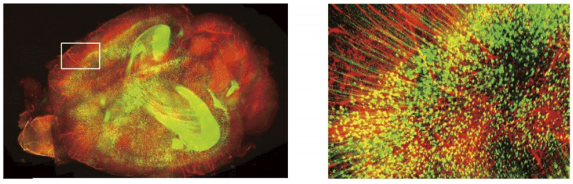
図1.透明化したマウス脳
ScaleS 法にて透明化した YFP-H マウス脳の 2 光子観察画像。血管を DyLight594 標識のトマトレクチンで標識。脳を切断することなく、脳神経の 1 本 1 本まで詳細な観察ができる。しかしながら、透明化した組織の実際の観察においては、対物レンズをはじめとする顕微鏡の観察能力は十分に生かされていない場合がある。生命科学の研究と共に顕微鏡の技術も発展してきたが、観察技術がより高度になればなるほど、顕微鏡は生命科学者にとって難しく、扱いにくいものとなってしまった。
今回は、光学の立場から、透明組織を観る光学系で最も重要な役割を担う対物レンズについて話をしてみようと思う。
屈折率と光の関係
光学観察において、屈折率は重要な要素の 1 つである。光の振る舞いは屈折率によって支配されているからである。スネルの法則(図 2(a))を覚えているだろうか?
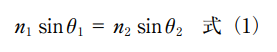
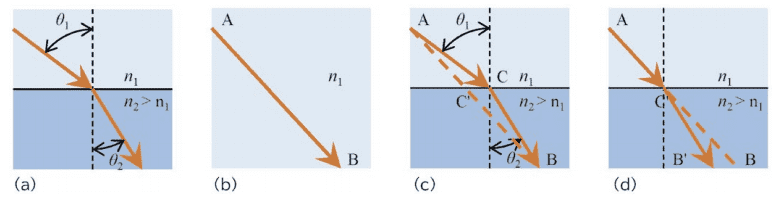
図2.スネルの法則とフェルマーの原理
(a)スネルの法則による屈折を示す。n2 は n1 より屈折率が高いためθ2 はθ1 より小さい。(b)~(d)フェルマーの原理を用いた屈折の説明。(b)では屈折率は均一なので、A から B の最短時間経路は直線となり光は直進する。(c)屈折率が途中で変化している場合を示す。A から B の最短時間は C を通る経路となり、光は界面で屈折する。この経路は(a)と一致する。(d)もし、光が A から C'(A から B へ直進したときに通る点)の光路を通った場合、最短時間となる経路は B' に到達する経路となり、B には到達しない。スネルの法則は、光学系がどれほど高度になろうが、必ず成り立つシンプルな基本法則である。屈折率が異なる2つの媒質の界面を通過するとき、光線は進む方向を変える。これを屈折というが、方向変化には法則性があり、それを数式化したものがスネルの法則である。なぜ光は屈折を起こすのか?これについては、ホイヘンスの原理に基づいた光の波動性から説明することもできるが、ここでは、別の視点から見てみよう。

図3.屈折率の違いによる見え方の違い
(a)スライドガラスを水に入れた場合。水(ne=1.33)とスライドガラス(ne=1.52)の屈折率が異なるため、スライドガラスが見える。また、水と空気の間の屈折によって、スライドラスが水面で若干曲がって見えている。(b)顕微鏡用のオイルに入れた場合。スライドガラスとオイル(ne=1.52)の屈折率が等しいため、スライドガラスは見えなくなってしまう。
光の進む速度は屈折率によって変わり、屈折率が高ければ高いほど、光はゆっくりとしか進めない(人が水中でゆっくりしか歩けないのと似ている)。図 2(b)のように点 A から点 B に光が進むとしたときに、光はどんな経路をとるか? 答えは、光は光学的距離が最短になる経路、すなわち進むのにかかる時間が最も短い経路を選ぶ。これをフェルマーの原理という。フェルマーの原理に従うと、光は屈折率の異なる界面を通る時には屈折を起こして進む方向を変える。そのほうが、直進するより早くたどりつけるからである。この時の屈折は、スネルの法則と等しい。
一方で、屈折率が同じであれば、たとえ媒質が異なっていても、光はその違いを判断できない。図 3 のように屈折率が同じガラスとオイルは区別がつかないので、オイルの中のガラスは見えない。組織の透明化にもこの原理が応用されており、組織の屈折率を一様に試薬の屈折率に近づけるように工夫がなされている。その結果として、透明化技術におけるマウンティング試薬の屈折率は非常に多岐にわたっている。それに応じて光学系も調整しなければならないことを想像していただけると思う。
球面収差
屈折率の変化が、光の集光にどのような影響を与えるかを説明しよう。図 4 は、レンズを使って光を 1 点に集光しているところを示している。集光の途中で屈折率が変わった場合、1 点に集まっていた光はどうなるであろうか? 光軸から離れた光線ほど、界面に入射する光の角度θは大きくなる。こうした光線群はスネルの法則に従い屈折し、進む方向を変え深さの異なる位置で光軸と交わる。結果、1 点には集光しない。
このように、本来 1 点に集光するはずの光がバラバラになって、1 点に集まらない現象を収差と呼ぶ。そして、図 4 で説明したような収差を球面収差という。球面の凸レンズで光を集光したときに、光が 1 点に集まらない現象に由来しているのでこのような名前がついている。
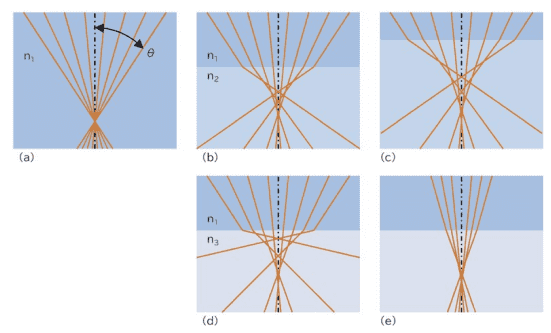
図4.屈折率差による球面収差発生の模式図
(a)均質な屈折率(n1)の媒質中で光が 1 点に集光している状態。球面収差は発生しない。(b)媒質の一部を低屈折率(n2)な媒質に置き換えた場合。球面収差が発生して、光は 1 点に集光しない。
(c)屈折率(n2)の媒質の深さが増えると、球面収差の量も増える。
(d)同じ深さでも、より屈折率が低い媒質(n3<n2)の場合は球面収差が増える。
(e)光線の角度が小さい部分で発生する球面収差は小さい。
球面収差の量は、次の 3 つに依存している。
(1)入射する光線の角度の大きさ。
(2)本来想定していた屈折率と、想定していない屈折率との差。
(3)想定していない屈折率の媒質を通る距離。
(1)は、角度の大きい光線ほど顕著になる。したがって、対物レンズのNA(開口数、Numerical Aperture)が大きいほど、球面収差も大きくなる。一般に、対物レンズの倍率が小さいと NA も小さく、倍率が大きいとNA も大きくなる。これは、NA が解像力に影響していることが関係している。
倍率が大きいということは、より細かいものを観察したいという意思のあらわれであり、そのため、光学系の解像力を高くすることが多い。低倍対物レンズで全体像を見るときには問題なかったはずが、いざ、高精細に観察しようとして高倍対物レンズに切り替えると、なんだか像がボケる、ということがあるが、これは、球面収差が影響していることが多い(図 5)。

図5.NA と倍率による球面収差の影響の違い
標本と対物レンズの間を空気で使うタイプの対物レンズを使ったワイドフィールド蛍光観察。ウシ肺動脈内皮細胞(BPAE cells)のミトコンドリアを Mito-Tracker Red で標識。画像下の数字は露光時間。露光時間の違いにも注目してほしい。(上段)適正な観察状態。NA が大きくなるにしたがって、細胞内のより詳細な構造の観察ができる。
(下段)カバーガラス 1 枚(厚さ 0.15mm)分の球面収差が発生した状態。10X(NA0.3)では上段との差はほとんど見られない。40X(NA0.95)ではコントラストが極めて悪く細胞内の構造がほとんどわからない。同じ 40X でも NA0.6 では、劣化の度合いは小さい。
(2)については、屈折率の差が大きいほど、光線は屈折によって本来通るべき方向から離れてしまう。水で使うはずの対物レンズにオイルを使っては、本来の解像力を得ることはできない。要するに、透明化試薬の屈折率に対応した対物レンズを使う必要があるが、透明化試薬の屈折率の数だけ対物レンズを用意しなければならない。
そこで、次に紹介する補正環という機構を用いることで、1 つの対物レンズで、ある程度の範囲の屈折率に対応することができるようになっている。
(3)は 3 次元イメージングを行うときに問題になる。一般に透明化された組織の屈折率は、透明化試薬によっておおよそ均一になっていると仮定できる。そのため、透明化組織内部で屈折率が変わることはあまりない。しかし、対物レンズと観察面との間では、屈折率の異なる媒質が存在することがある。例えば、倒立顕微鏡で標本を下から観察する場合、標本を容器に入れる。容器の内側は透明化試薬で満たされており、屈折率は透明化試薬のものとなる。
一方で、容器と対物レンズの間を満たす液(これを浸液という)は、透明化試薬と同じでなくても構わないため、水やシリコーン、オイルなどが用いられ、透明化試薬とは屈折率が一致しない。このような場合、観察深度が変わると、対物レンズから観察面までの間の、屈折率の異なる媒質の占める割合が変化する。この割合が変わると、発生する球面収差の量も変わる。
このような場合には、そのつど球面収差を補正するか、透明化試薬と浸液の屈折率を同じにそろえるという解決策がある。また、容器そのものの屈折率は、透明化試薬とも、浸液とも異なるため、容器に由来する球面収差も考慮しなければならない。
この収差によるボケの影響は、共焦点顕微鏡や、2 光子励起顕微鏡を使った観察をする場合には、より大きな問題となる。共焦点顕微鏡では、励起光を標本の 1 点に集光し、その 1 点から発せられた蛍光は極小のピンホールを通して検出される。球面収差の発生によって集光が乱れると、励起光、検出光のどちらも広がってしまい、効率が著しく低下する。また、2 光子励起顕微鏡では、2 光子励起の起こる確率は光の強度の 2 乗に比例している。そのため、集光が乱れると、急速に 2 光子励起効率が低下して、観察画像の S/N が劣化する。
対物レンズと補正環
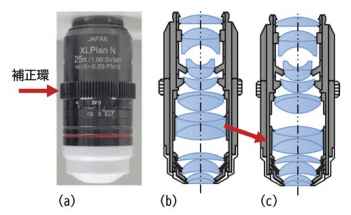
図6.補正環の調整とレンズの動き
(a)補正環付き対物レンズの例。 (OLYMPUS XLPlanN25XSVMP)(b)(c)補正環を回したときのレンズの移動の模式図。
補正環を回すと、対物レンズ内の一部のレンズが光軸方向に移動する。これにより、対物レンズ自身の球面収差量を変え、標本で発生する球面収差をキャンセルする。
前述の球面収差を補正し、高精細な観察を行うために、異なる仕様の対物レンズが複数用意されている。また、これらの対物レンズには補正環と呼ばれる機構がついていることがほとんどである。補正環は、対物レンズ内の一部のレンズを移動させる(図 6)ことにより、対物レンズ内を通る光線の屈折を変え、球面収差によって乱れて しまった光の集光を補正して、再び 1 点に集光させる機構である。
図 7 はSCALEVIEW-A2、SCALEVIEW-Sでそれぞれ透明化した組織を観察している例を示している。使用する対物レンズ XLPLN10XSVMP は補正環を備えている。カバーガラス(厚み 0.17 mm、ne=1.52)の有無や、SCALEVIEW-A2(ne=1.38)と SCALEVIEW-S(ne=1.49)の屈折率の違いによって球面収差が発生するが、補正環を適切に調整することによって、球面収差を補正し、再び 1 点に集光することが可能である。ただし、補正環による球面収差の補正には限界があり、どんな透明化試薬にも対応できるわけではない。対物レンズがどの透明化試薬に対応しているかは、各メーカーに問い合わせて相談することが望ましい(図 8)。
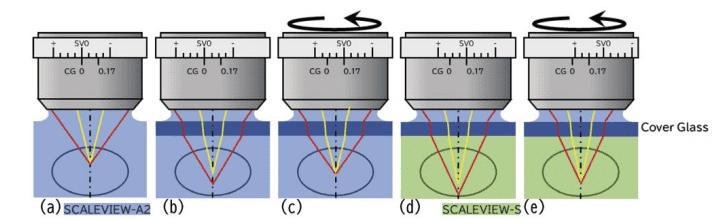
図7.透明化試薬及びカバーガラスの影響と補正環による補正
(a)SCALEVIEW-A2 で透明化した標本を観察している状態。補正環を調整し、球面収差は発生していない。(b)カバーガラス越しの観察。カバーガラスの屈折率がSCALEVIEW-A2 よりも高いため、球面収差が発生している。(d)SCALEVIEW-S で透明化した標本を観察している状態。SCALEVIEW-A2 とは屈折率が異なるため同じ補正環の位置では球面収差が補正されていない。(c)(e)補正環を調整することで、球面収差が補正される。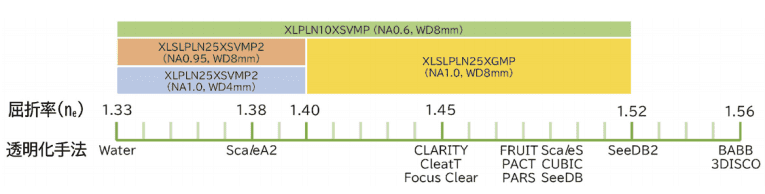
図8.透明化試薬の屈折率と対応対物レンズ
透明化試薬は ScaleA2 の 1.38 から BABB の 1.56 までと幅広い。OLYMPUS では主に水溶性の透明化試薬に対応する対物レンズをラインナップしている。しかしながら、この補正環は有効に使われていないことが多い。補正環の存在そのもの、あるいは補正環の機能を知らないため、使っていない場合がある。また、補正環調整の難しさから、使うことをあきらめていることもある。補正環の調整は、画像を見ながら人が感覚的に一番良いところを探さなければならないが、補正環を動かすとピント位置も動いてしまうことが多く、ピント合わせと補正環調整の両方を同時に行わなければならない。この作業には熟練が必要で、最適な状態を見つけ出すことが難しい。

図9.TruResolution システム用対物レンズ
補正環を電動で駆動し、画像解析を行うことで、補正環の最適な位置を自動で判別する。また、観察する深さの変化に連動して自動で補正環を最適な位置に調整する。また、3次元イメージングを行う場合には、前述のように観察深度によって球面収差が変わるため、深さを変えるたびに補正環を調整しなければならない。これは現実的ではないため、実際は補正環をある位置で固定したまま使われている場合がほとんどである。
このような課題を解決し、対物レンズが持つ本来の解像力を十分に発揮するために開発されたのが OLYMPUS の TruResolution システムである(図 9)。本システムでは、補正環の最適位置を画像から自動で判断して調整し、また、深さの変化に応じて連動して駆動する仕組みが組み込まれている 5)。これにより、補正環を意識することなく、最適な画像を常に得ることができる。
深さ位置の乖離
球面収差のほかにも、注意する点がある。図 10 は観察深度を変えながら画像を取得している状態を表しているが、集光する位置に注目してもらいたい。対物レンズの移動距離Δd と集光位置の移動量ΔD は同じではなく、以下の関係にある。
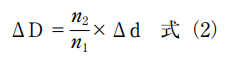
この現象は、対物レンズの NA が小さく球面収差が無視できる状態や、補正環で球面収差を補正した状態でも発生する。観察装置が制御し把握できるのはΔd だけであり、この情報を使って 3 次元像を再構築する。そのため、屈折率 n1、n2 の比によって、再構築される画像が観察方向に圧縮または伸長された形となる。
また、ライトシート顕微鏡では、照明光は観察用の対物レンズとは異なる別のレンズを使って、標本の横側から照明する。照明光の位置は、観察面の移動に対応して動かさなければ、照明光と観察面とが異なってしまい観察できない。これらの問題を解決するには、式(2)を使った補正を行う。そのためには、浸液と透明化試薬の屈折率を把握しておくことが重要である。
終わりに
今回、光学の立場から、組織透明化と対物レンズについて解説した。普段馴染みのない項目が多く戸惑ったかもしれない。今後も組織透明化の技術は発展し、アプリケーションも広がっていくと思われる。しかし、透明化しただけでは必要な情報を得ることはできず、そこには必ず観察の技術が必要となる。各顕微鏡メーカーの WEB ページにも、光学の解説がされており参考にしていただければと思う。本解説が、透明化技術を使ったイメージングの発展の一助になれば幸いである。
参考文献
- Eugene Hecht:「原著 5 版ヘクト光学Ⅰ 基礎と幾何光学」(丸善出版)(2018).
- Eugene Hecht:「原著 5 版ヘクト光学Ⅱ 波動光学」(丸善出版)(2018).
- 田所利康:「イラストレイテッド 光の実験」(朝倉書店)(2016).
- 「顕微鏡を学ぶ」, OLYMPUS ホームページ https://www.olympus-lifescience.com/ja/support/learn/
- Ue, Y. et al. : Biochem. Biophys. Res. Commun., 500, 236 (2018).
シリーズ終了にあたって
本シリーズは、透明化技術を正しく普及することを目的として、各技術の基礎知識、観察方法、応用方法、適切な対物レンズの選び方、実際のイメージング事例を紹介してきました。現在、透明化技術を用いたアプリケーション報告は国内外で活発に行われています。透明化技術の発展は、透明化技術を含めたイメージング分野で世界をリードする多くの日本人研究者と日本の顕微鏡メーカーが大きく貢献してきた背景があり、世界の最先端イメージング技術の基盤が日本にはあります。今後、日本発技術を用いた透明化技術アプリケーションが大きく広がっていき、生命科学研究での新しい知見が生まれることを大いに期待したいと思います。また、本シリーズへの寄稿を快諾いただいた方々に、この場を借りて感謝を申し上げます。









